“I like that he’s having fun. I just need him to know how wrong he is.”

Mr GrumpyKitten

Introduction

My dad loves Camel Up. Seriously, this is a game that has brought him countless hours of joy. Despite our expensive game collection, it’s the one that he always requests. For most Millennials obsessed with games – this is a great situation. Your parents are willingly sitting down to the table to play with you? Mission Accomplished!

The problem is that I hate the way he plays. He constantly picks up that surprisingly satisfying plastic pyramid and rolls the dice. He even does this when we casually observe out-loud that Blue is certainly going to win the leg and there’s a Blue-3 betting tile just sitting there. He just wants to know what happens next! Don’t get me wrong – I like that he’s having fun. I just need him to know how wrong he is.

In this series, we’ll dive deep into Camel Up using mathematics & Python. You’ll learn enough along the way to thrash your family at your next games night! Who said mathematics was useless?

A project was born

And so, a project was born: armed with my trusty degree in Math and seven years as a software engineer I sat down to prove how misguided he is. So, I reached for my favourite serpentine hammer and started building.

I modeled the game using Python, creating an environment where the game can be simulated using players with some straightforward strategies. You can check out the code on my GitHub here.

Right now, I’ve implemented a simplified version of the rules. For the time-being we won’t worry about the boost tiles, end of game betting, or the crazy camels from the second edition. I’ll add these in later. For now, this is sufficient to start asking (and answering) some questions about the fundamental structure of the game. (Need a refresher on the rules? Take a look here).

Current Implementation

Right now, on an player’s turn, they can either:

• Roll the Dice,
• Take a Leg Betting Tile.

Using these, I’ve devised two simple strategies for my horde of simpleton automated monkeys to carry out:

1. Roll the Dice (also known as the Dad Strat)
   – Just roll the dice every turn and enjoy last place!
2. Take Leader’s Betting Tile, Otherwise Roll Dice
   – Actually uses a little bit of logic!
   – If any of the current leader’s betting tiles are available then take one, otherwise default to rolling.

First Question

With the above, we can start to ask questions about the game at a fundamental level.
The first one: how many legs does the game usually last?

Let’s start with the theoretical minimum and maximum number of legs. Believe it or not, it is supremely unlikely but perfectly possible for the game to end on leg one! The maximum length is a whopping 16 turns. Personally – this sounds worse than a game of Settlers of Catan, but only just.

Skeptical? I don’t blame you but I swear I have evidence to back it up! If you’re feeling in a problem-solving mood, try to prove this yourself! Otherwise, I’ve included the full argument as a treat at the end of the post.

Distribution of the Number of Legs

I’m going to throw out some claims so I can look like a genius when the data proves me right:

Claim 1 – The number of legs in the game is independent of the number of players

• Camels only move when a die is rolled which happens five times per leg no matter how many players.
• This is false when boost tiles are available. There can be as many tiles on the track as players which alters the distribution.

Claim 2 – The average number of legs should be less than 15 / 2 = 7.5 legs

• A camel must travel 17 spaces in total to win the game. The dice rolled each turn has an average value of 2. There is a free roll at the beginning of the game during set-up.
• Therefore, on average, a camel only needs to travel 15 spaces to win the game, which will take 7.5 legs using the average value of the dice.
• It should be less than 7.5 due to the stacking of the camels. Stacked camels can move twice (or more!) per turn.

Claim 3 – The distribution of the number of legs should be independent of player strategies

• The leg ends once all the dice have been rolled. A player’s strategy affects the number of turns in the leg, but not the number of legs.
• This is ignoring the boost tiles for now. But didn’t I already tell you to ignore those?

I simulated a whopping 100,000 games at each player count from 2-5 players (400,000 games total). Then, I made a pretty graph which you can see below. If you want to see how this is done you can follow along here.

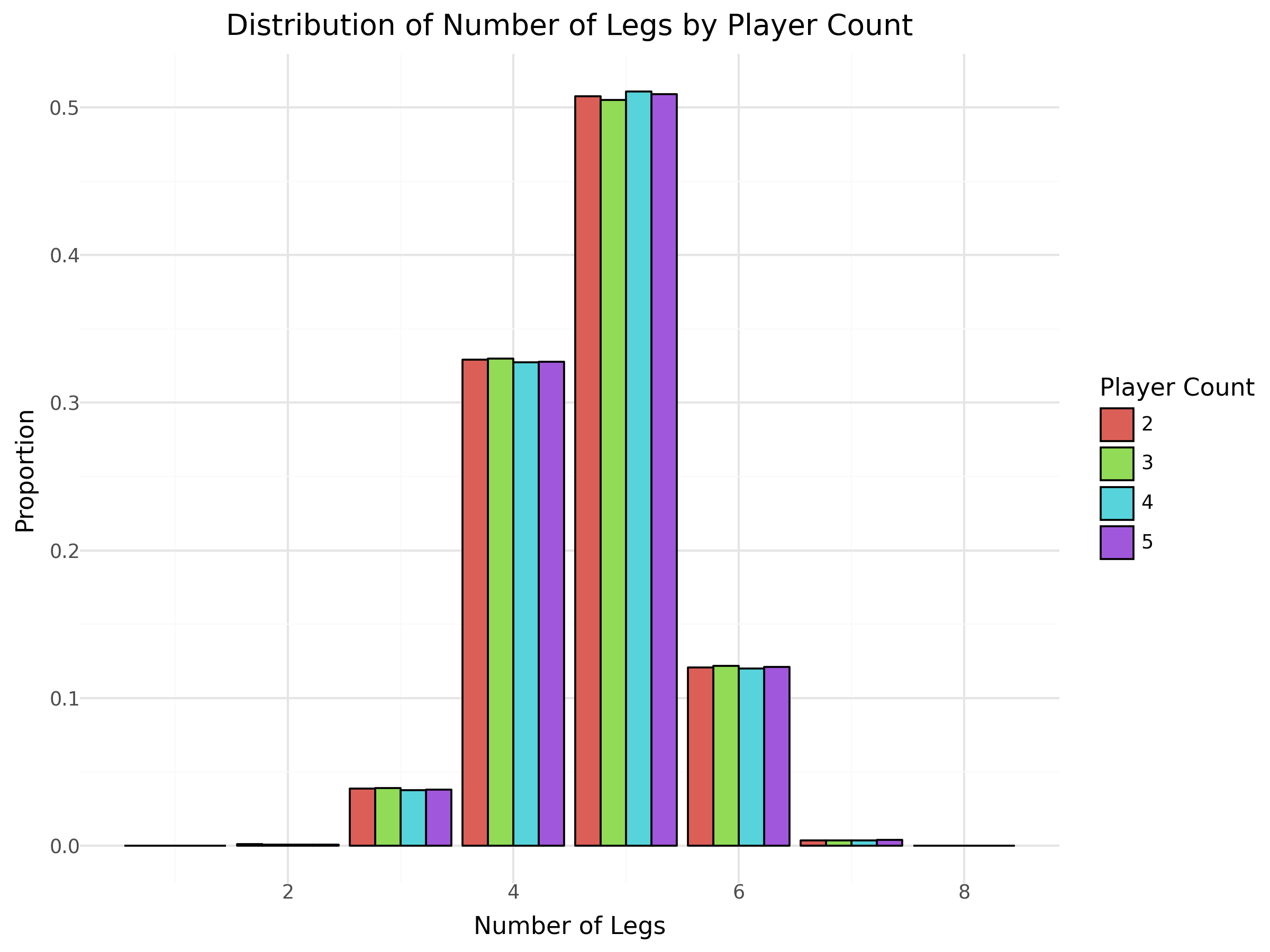
Let’s compare the results with the claims.

Claim 1 – The number of legs in the game is independent of the number of players

The chart shows that the distribution is consistent as the bars are the same height regardless of the player count. This validates claim 1. Good job GrumpyKitten.

Claim 2 – The average number of legs should be less than 15 / 2 = 7.5 legs

The average number of legs is 4.72 which is less than 7.5 as expected. Including the free roll during set-up, this implies that the winning camel travels (17 – 2) / 4.72 = 3.17 spaces per turn on average. This is only possible if the camel is a beneficiary of some stacking!

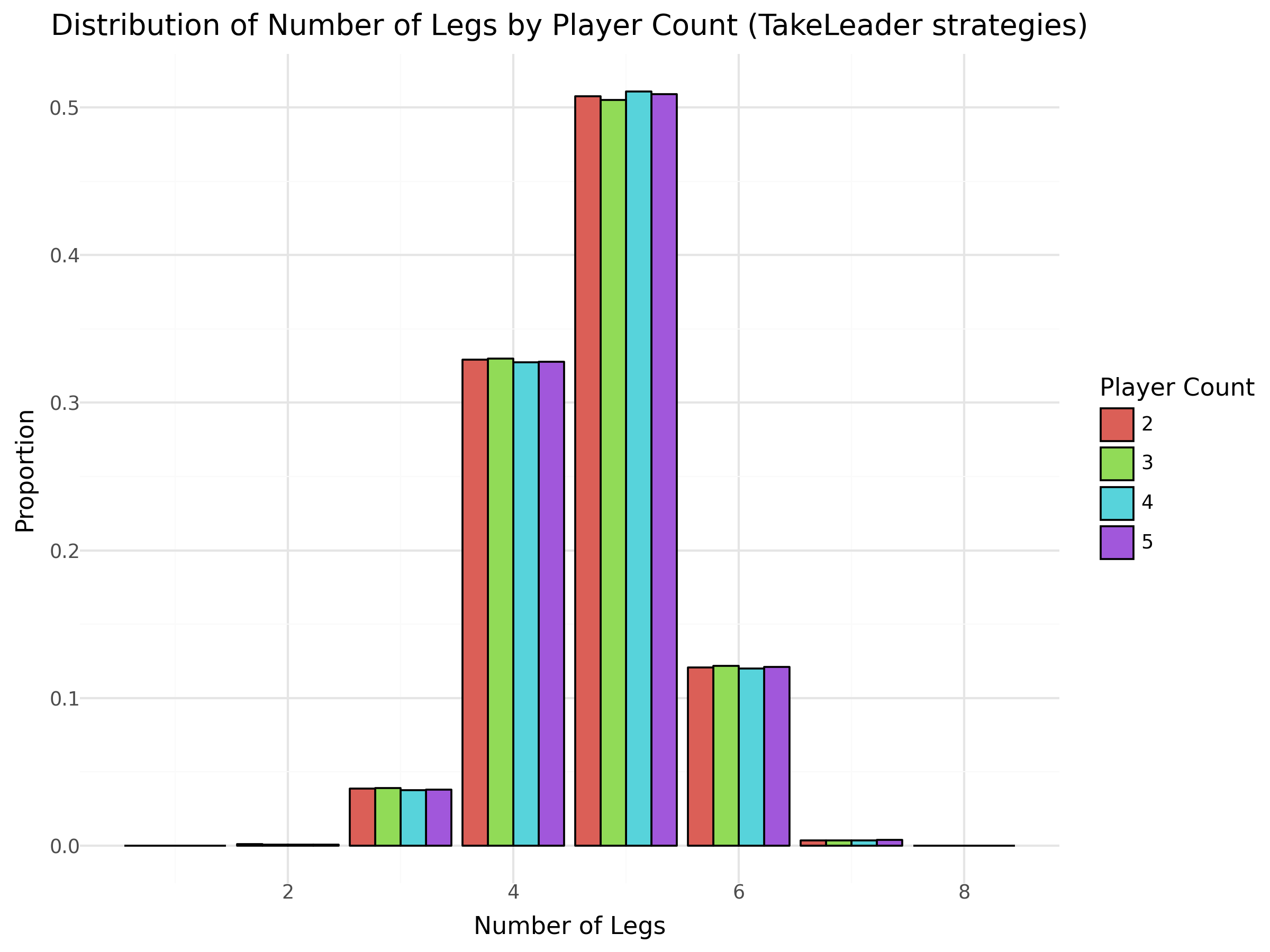
Claim 3 – The distribution of the number of legs should be independent of player strategies

To try to argue this claim I repeated the simulation above with all agents having a different strategy. This yielded yet another pretty graph! I gave the agents the TakeLeaderBettingSlip strategy instead of the AlwaysRollDice strategy. What we see is that the distributions are almost identical between the two strategies.

This, along with the theoretical argument above, provides us with some proof that the player strategies do not alter the number of legs in the game.

Takeaways

We’ve learned some lessons about the underlying structure of a game of Camel Up. We learned about how many legs a game will last (4-5 on average). We’ve also explored some ideas about how player strategies don’t affect the number of legs. Unless. of course, you’re manipulating things with your boost tiles!

So what does this mean for your family game night? With our new understanding of the game’s dynamics you can plan your moves more strategically – especially when it comes to timing your end-of-game betting cards. Over 90% of the time the game will end at either 4, 5, or 6 legs. If you’re on leg 4 – you should really think about end-of-game betting . With a high player count the game can end before you have enough turns to make your bets.

When you win your next game, you’re welcome. Ready for more? Let’s see where this is going next!

Where Next?

The next post in this series will tackle two questions:

1. Does going first actually matter?
   – A dive into how player order affects win probabilities in this toy example.
2. How much does a simple betting strategy outperform rolling the dice?
   – Spoilers: A LOT.

We’ll continue to add to our model and answer interesting questions as we go further through the project. We’ll also look later in the series at how to train a reinforcement learning algorithm using gymnasium to play Camel Up!

Appendix – Derivations of the Min / Max Number of Turns

Minimum Number of Legs

Believe it or not, it is possible (but supremely unlikely) for a camel to cross the finish line on leg 1.

Consider a scenario where:

1. All five camels stack on space 3 during set-up,
2. Dice come out of the pyramid in order from the bottom to the top of the stack,
3. Every roll is a 3.

The total distance that the camel on top of the stack will move is a staggering 5 * 3 = 15 spaces! Including the 3 from set-up yields 18 spaces – enough to win the game!

Maximum Number of Legs

In another unlikely scenario, it can take 16 legs for a camel to cross the finish line.

Imagine:

1. All five camels roll a 1 during set-up,
2. The dice exit the pyramid from top-to-bottom of the stack,
3. All dice rolls are 1s.

Then each camel moves exactly 1 space during the leg. Repeating this and remembering the 1 space from setup gives 16 legs for our camels to labour to the finish line.

Calculating the probabilities of the above occurring is left as an exercise to the reader. I will note that the charts above have no games that ended on leg 1.