Recently I’ve been spending a lot of time thinking about the board game Camel Up. If you’ve missed it – check out the series starting here: How to Beat Your Dad At Camel Up. One observation from my last article about reinforcement learning was that the number of game states is very large. This means our agent needs to play the game many millions of times to see all possible states. This led me to the question – how many board states, exactly, are there?
Why does this matter? Well, if we know how many states there are, we can target how many games to play during training. If the number is unreachable given our setup – it will also tell me if I must be smarter about updating the Q-table (expected future reward from an action given the game state).
Let’s start with some naive results. If we assume that:
- the positions of the camels on the board is a vector of length 5,
- each camel can be on one of the 17 squares independently of all others,
- ignoring stacking, for the moment,
then we have 17 options for each of the camels, so the number of combinations would be ![]() . Not all of these are possible combinations. For example, it’s not possible to have 4 camels on space 16 and one camel on space 1, as there are no combination of die rolls that results in that board state. It’s also dependent on the leg, it’s impossible to have camels on space 1 in the 5th leg. We’re going to call allowed board states admissible.
. Not all of these are possible combinations. For example, it’s not possible to have 4 camels on space 16 and one camel on space 1, as there are no combination of die rolls that results in that board state. It’s also dependent on the leg, it’s impossible to have camels on space 1 in the 5th leg. We’re going to call allowed board states admissible.
Definition: A board state is admissible if there is a possible sequence of legal moves that will produce that board state. If no such sequence exists then the board state is inadmissible.”
So we want to answer the question: how many admissible board states are there?
We’re not going to answer that exact question today. However, I want to lay out my thoughts on tackling this problem and present some initial work on a sub-problem.
How to Tackle The Camel?
There are some standard ways in mathematics to try to answer such a question:
- Write out every possible configuration:
- This is going to take forever, and there’s a high chance of making mistakes. Probably not a good option for us.
- Upper & Lower Bound Convergence:
- This is a classic technique. We find some lower bound on the number of possible states, and a companion upper bound. We then try to improve these bounds to make these meet. For example, we know there is at least 1 admissible board state. So, 1 will be our lower bound to start with. We know there are 1,419,857 possible states (excluding stacking), so the answer lies somewhere between those two numbers.
- How can we make progress? We can use simulation to greatly increase our lower bound. If we see it in a simulation – then it’s an admissible state! For the upper bound we will need to make arguments on which states are possible or not.
To make a theoretical argument on which states are possible, it will be useful to understand how the camels move. For example, if we know there is no way for two camels to both move 16 spaces in one leg then we know that ![]() is an inadmissible board state on leg 1.
is an inadmissible board state on leg 1.
How Many Ways Can a Camel Move Spaces?
Let’s start with an easier sub-problem. Given a camel on a space, in how many ways can it move ![]() spaces in a leg? For example, a camel can move 1 space in 1 way, if it rolls a 1. It can move 2 spaces in 2 ways: if it rolls a 2, or if there is a camel underneath it that rolls a 1, and then our top camel rolls a 1. This is dependent on how many camels are potentially under the camel. If it is the only camel on the board, then it can only move a maximum of 3 spaces (and it’s guaranteed to win!). If there are 4 other camels that can potentially boost it up the board, then it can move significantly farther.
spaces in a leg? For example, a camel can move 1 space in 1 way, if it rolls a 1. It can move 2 spaces in 2 ways: if it rolls a 2, or if there is a camel underneath it that rolls a 1, and then our top camel rolls a 1. This is dependent on how many camels are potentially under the camel. If it is the only camel on the board, then it can only move a maximum of 3 spaces (and it’s guaranteed to win!). If there are 4 other camels that can potentially boost it up the board, then it can move significantly farther.
To put some nomenclature around this to make it easier – I’m going to refer to the camel that’s moving as the target camel. We are not conditioning on any game state, so this distribution will make no assumption on whether there is a camel underneath the target camel or not. We will refer to this as a possible camel.
We can derive a recurrence relationship for the number of ways the target camel can move using dynamic programming:
Definition: Let
be the number of ways a target camel can move
spaces with
possible camels underneath it.
I posit that the recurrence relationship to generate these is as follows:
![]()
That is, the number of ways for the target camel to move ![]() spaces is the number of ways for a possible camel underneath our target camel to move sufficient spaces so that our target camel can roll a one, two, or three to get to the desired space. The possible camel underneath can have at most one fewer possible camel underneath it, as we know our target camel is on top of the possible camel.
spaces is the number of ways for a possible camel underneath our target camel to move sufficient spaces so that our target camel can roll a one, two, or three to get to the desired space. The possible camel underneath can have at most one fewer possible camel underneath it, as we know our target camel is on top of the possible camel.
Given this, we can derive some initial conditions for ![]() and then use those to derive the entire distribution!
and then use those to derive the entire distribution!
If there are no possible camels underneath our camel, then this camel can move 1, 2, or 3 spaces in exactly one way each. The only possible way is to roll that number on the die and move that many spaces. Therefore:
![]() . For completeness,
. For completeness, ![]() for
for ![]() and
and ![]() for
for ![]() .
.
We can now sort out the ![]() case, where there can be at most one possible camel. The target camel can still move 1 space in exactly 1 way, rolling a 1. However it can now move 2 spaces in 2 ways: rolling a 2, or a possible camel rolling a one followed by the target camel rolling a 1.
case, where there can be at most one possible camel. The target camel can still move 1 space in exactly 1 way, rolling a 1. However it can now move 2 spaces in 2 ways: rolling a 2, or a possible camel rolling a one followed by the target camel rolling a 1.
We illustrate by applying our recurrence formula for the ![]() case:
case:
![]()
![]()
![]()
![]()
![]()
![]()
We can tabulate the higher values of ![]() using Python.
using Python.
from collections import defaultdict
# Using a defaultdict to avoid having to check if value has been set.
output = defaultdict(lambda: defaultdict(int))
# Set c=0 values.
output[0][1] = 1
output[0][2] = 1
output[0][3] = 1
for c in range(1, 5):
for x in range(1, 17):
output[c][x] = output[c-1][x-3] + output[c-1][x-2] + output[c-1][x-1] + (1 if 1 <= x <= 3 else 0)
Running this code results in the distributions below:
| x / c | c = 0 | c=1 | c=2 | c=3 | c=4 |
| x=1 | 1 | 1 | 1 | 1 | 1 |
| x=2 | 1 | 2 | 2 | 2 | 2 |
| x=3 | 1 | 3 | 4 | 4 | 4 |
| x=4 | 3 | 6 | 7 | 7 | |
| x=5 | 2 | 8 | 12 | 13 | |
| x=6 | 1 | 8 | 18 | 23 | |
| x=7 | 6 | 22 | 37 | ||
| x=8 | 3 | 22 | 52 | ||
| x=9 | 1 | 17 | 62 | ||
| x=10 | 10 | 61 | |||
| x=11 | 4 | 49 | |||
| x=12 | 1 | 31 | |||
| x=13 | 15 | ||||
| x=14 | 5 | ||||
| x=15 | 1 |
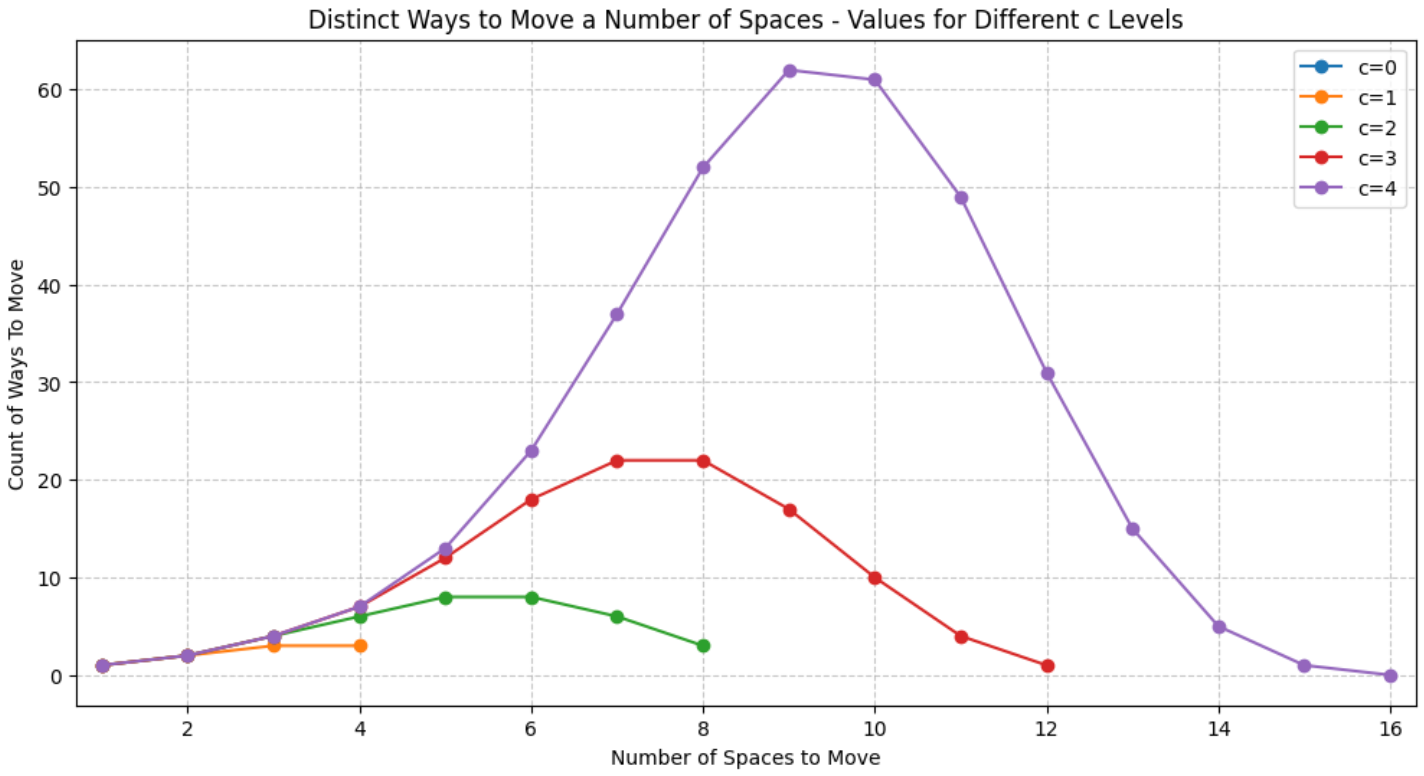
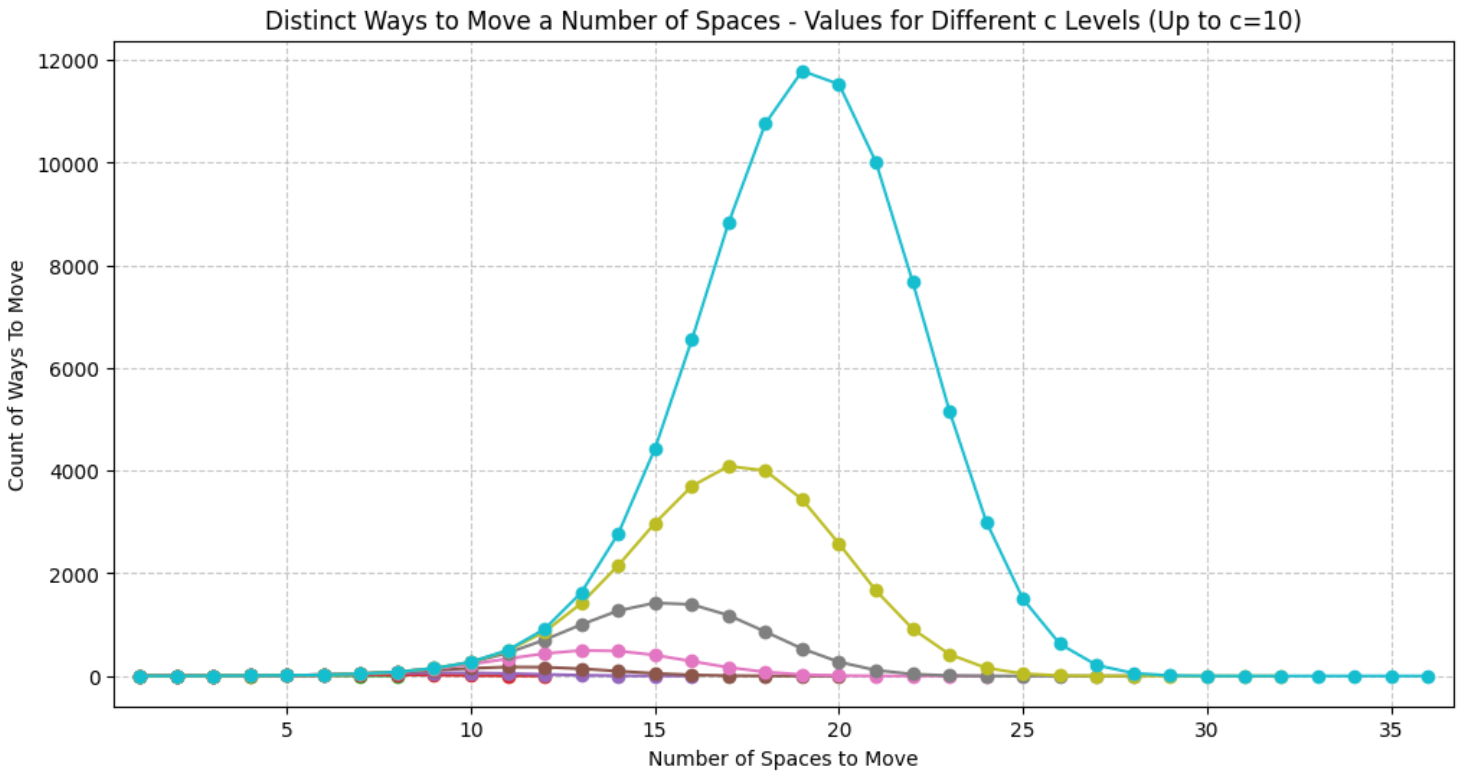
We can see the peak of the distribution move to the right as ![]() increases. It also starts to look pretty bell-curvy. As
increases. It also starts to look pretty bell-curvy. As ![]() increases, the mean converges to
increases, the mean converges to ![]() as shown on the graph below.
as shown on the graph below.
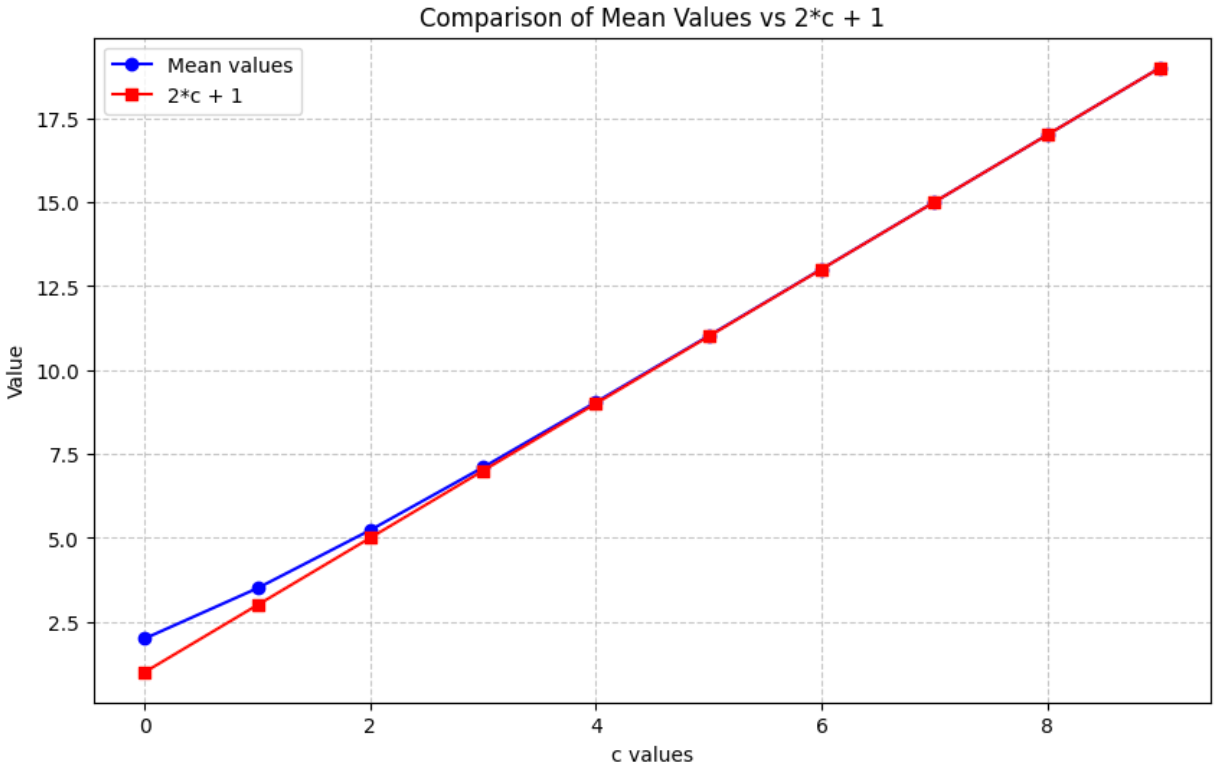
I’ve been unable to experimentally find a function for the standard deviation as ![]() increases. I’ve tried fitting a power law of various forms and nothing quite fits. I’ll continue to work on that one over the coming weeks.
increases. I’ve tried fitting a power law of various forms and nothing quite fits. I’ll continue to work on that one over the coming weeks.
Takeaways & What’s Next?
In this article I’ve derived the distribution of the number of ways that a camel can move a number of spaces. This is not yet of much practical benefit for your game night! We’re much more interested in the distribution of the number of ways a camel can move given an initial game state. However, this is a first step.
Where am I hoping that this will lead? I’m hoping that this will help answer these questions:
- How many admissible game states are there? As noted above, this will have implications on how the state is represented for reinforcement learning.
- What practical tips are there for playing Camel Up? I want to derive some heuristics from this result that will help players in their family games nights.
- What’s the limiting distribution as
 ? I conjecture that the limiting distribution will be Normal with mean
? I conjecture that the limiting distribution will be Normal with mean 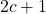 ; however, the standard deviation is still an open question. Figuring out exactly how to prove this analytically will be a next step.
; however, the standard deviation is still an open question. Figuring out exactly how to prove this analytically will be a next step.
Stay tuned for the next article to start figuring out the answers to these questions! Subscribe today so that you don’t miss an article.
Leave a Reply